博客文章标记求解器系列
改善多物理问题的收敛性
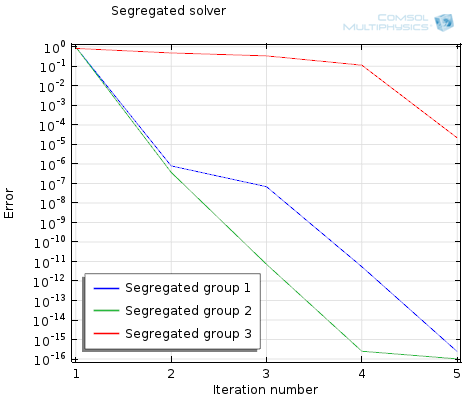
在我们以前的博客条目中,我们介绍了用于解决comsol中稳态多物理问题的完全耦合和隔离算法。188金宝搏优惠在这里,我们将研究加速这两种方法的收敛技术。
解决多物理问题
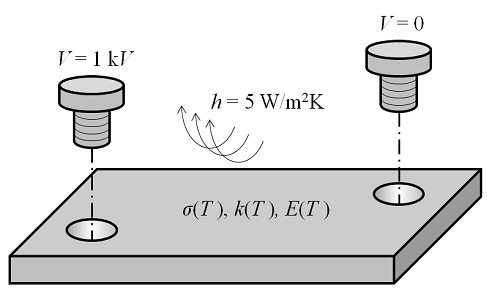
在这里,我们介绍了用于解决comsol多物理学中多物理有限元问题的两类算法。188金宝搏优惠到目前为止,我们已经学会了如何与线性和非线性单物理有限元问题进行网络和求解,但尚未考虑当在同一域内解决多种不同的相互依存的物理学时会发生什么。
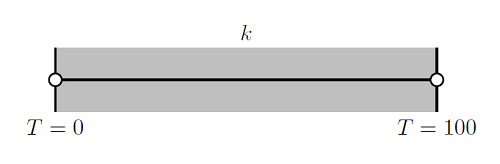
非线性静态有限元问题的网格划分注意事项
作为求解器博客系列的一部分,我们讨论了解决非线性静态有限元问题,改善非线性问题收敛性的负载渐变以及非线性渐变以改善非线性问题的收敛性。我们还引入了线性静态问题的网格划分考虑,以及如何识别奇异性以及在网格划分时该如何处理它们。在这些主题的基础上,我们现在将讨论如何准备网格以有效地解决非线性有限元问题。
非线性渐变以改善非线性问题的收敛性
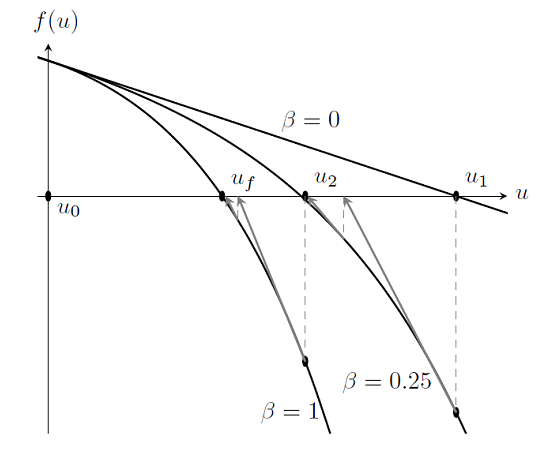
正如我们在“非线性问题的负载渐变”中看到的那样,我们可以使用持续方法从我们知道解决方案的卸载情况下将问题上的负载升起。该算法对于理解失败负载附近发生的事情也很有用。但是,在所有情况下,负载坡道均不会起作用,也不效率低下。在这篇文章中,我们介绍了提高问题中非线性以改善收敛性的想法。
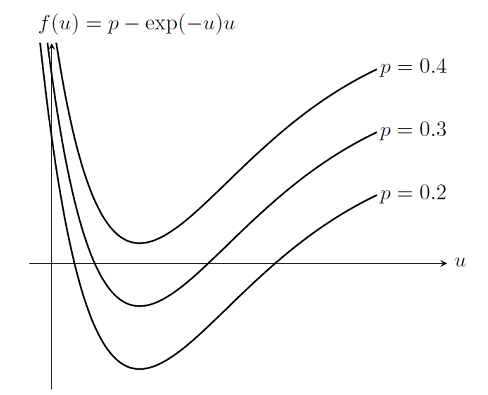
非线性问题的负载渐变
正如我们之前在博客条目中看到的有关解决非线性静态有限元问题的文章,并非所有非线性问题都可以通过抑制的Newton-Raphson方法来解决。特别是,选择不正确的初始条件或无需解决方案设置问题,只会导致非线性求解器继续迭代而无需融合。在这里,我们介绍了一种更强大的方法来解决非线性问题。
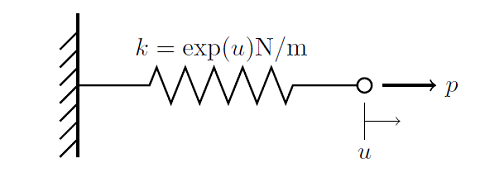
解决非线性静态有限元问题
在这里,我们开始概述用于解决非线性静态有限元问题的算法。此信息是在非常简单的一维有限元问题的上下文中介绍的,并建立在我们先前关于求解线性静态有限元模型的条目上。
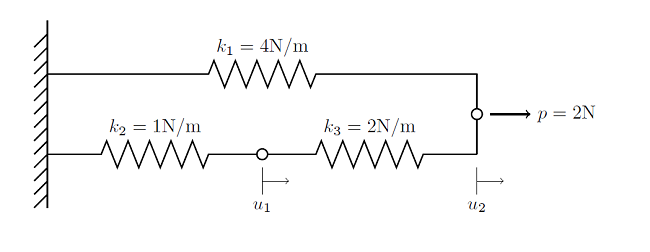
方程式线性系统的解决方案:直接和迭代求解器
在此博客文章中,我们介绍了Comsol中使用的两类算法,用于求解解决任何有限元问题时出现的线性方程系统。188金宝搏优惠这些信息与理解求解器的内部运作以及了解记忆需求如何随着问题大小增长而言是重要的。
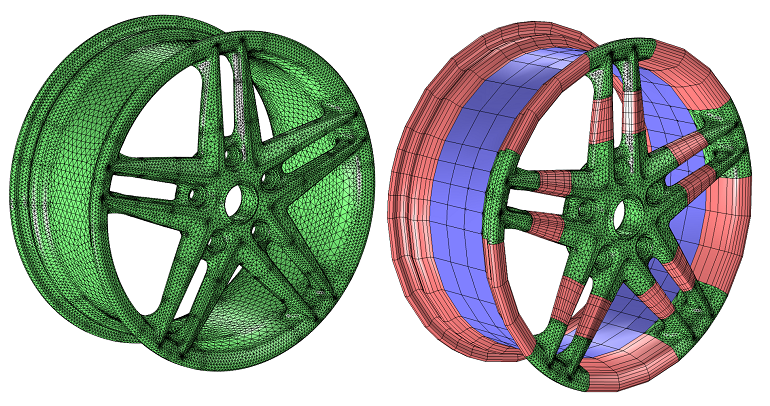
网际几何形状:何时使用各种元素类型
在以前的博客条目中,我们介绍了线性静态问题的网格划分注意事项。关键概念之一是网状融合的想法 - 当您完善网格时,解决方案将变得更加准确。在这篇文章中,我们将更深入地研究如何选择适当的网格以开始您的网格收敛研究,以解决线性静态有限元问题。
